The bifurcation of sub-waves in space and time
• Is the bifurcation of sub-waves a process in space or in time, or both?
• How are elementary matter- and force particles formed?
• What is the role of the potential well?


In sub-wave / microvita theory, the bifurcation of sub-waves in space and in time is closely interwoven, but each is treated differently.

The bifurcation in space, (B) subjective > (B) objective, constitutes a spectral analysis of the source wave numbers (cycles per unit of distance) and is initially manifested through the formation of matter-waves.

3 source sub-waves
4 bifurcated sub-waves
sub-wave #
wave number
angular velocity
1
Phi^0 = 1
1
2
Phi^1 = Phi
1
3
Phi^2
1
sub-wave # wave number angular velocity
0 - electron Phi^2 - Phi - 1 = 0 1 - 1 - 1 = -1
1 - photon Phi^2 - Phi + 1 = 2 · 1 1 - 1 + 1 = 1
2 - gluon Phi^2 + Phi - 1 = 2 · Phi 1 + 1 - 1 = 1
3 - quarks Phi^2 + Phi + 1 = 2 · Phi^2 1 + 1 + 1 = 3

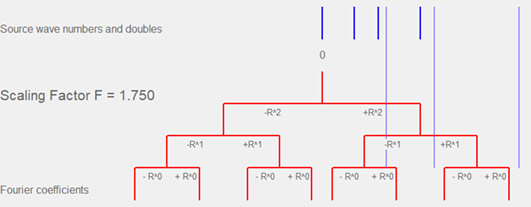
Integral bifurcation table, with emphasis on spacial bifurcation. Only non-negative wave numbers are considered.
Note the factor 2 each time - this is the wave number bifurcation, only occuring at Phi (1.618) synchronized scaling.


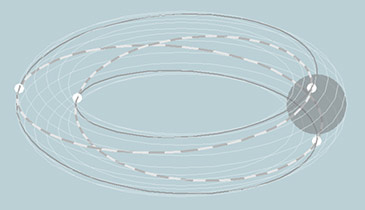
The common angular velocity (or phase or frequency) of the source sub-waves bifurcates in time: (A) subjective > (A) objective. It manifests through the formation of a spherical potential well in which the matter-wave or -particle moves in a closed trajectory.

Increasing curvature of the matter wave, while space-time is transformed into a potential well with a nucleus.
Note that unlike in philosophy, the straight flow ("nada") also has an inner oscillation - this is the sub-wave.


The matter-wave is 1-dimensional, implying a bound sub-wave with unit angular velocity (1 electron). The nucleus (incl. its surrounding medium), is 3-dimensional, implying a bound sub-wave with triple angular velocity (3 quarks).


3 source sub-waves
4 bifurcated sub-waves
sub-wave #
wave number
angular velocity
1
Phi^0 = 1
1
2
Phi^1 = Phi
1
3
Phi^2
1
sub-wave # wave number angular velocity
0 - electron Phi^2 - Phi - 1 = 0 1 - 1 - 1 = -1
1 - photon Phi^2 - Phi + 1 = 2 · 1 1 - 1 + 1 = 1
2 - gluon Phi^2 + Phi - 1 = 2 · Phi 1 + 1 - 1 = 1
3 - quarks Phi^2 + Phi + 1 = 2 · Phi^2 1 + 1 + 1 = 3

Integral bifurcation table, with emphasis on angular velocities.

MOVE OVER OR TAP IMAGE TO START

MOVE OVER OR TAP IMAGE TO START

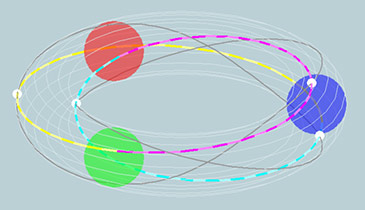
Electron- and quark (Dirac) spinors, modeled as resp. (2, -1) and (2, -3) toruses.
The dashed tracks are the electric resp. accurate "color" charges, both a (2, 1) torus.
The white nodes show the interdigitation between the matter- and force- spinors.
In the current gauge the charge is cycling whereas the particles are still.


The potential-well is 2-dimensional, it is a topological- or surface phenomenon which constitutes the charge. The associated particles are the photon resp. gluon, force-carriers. The spherical potential well is nothing but the (space and time) bifurcation itself in dimensional form.

The spherical shell or surface-area, in a general sense, accounts for the source sub-waves' common phase cycle, bifurcating in self-interactive, quadratic form, and therefore with dual angular velocity. The source phases and the topologically bifurcated phases together form a resonant potential well.


MOVE OVER OR TAP IMAGE TO START
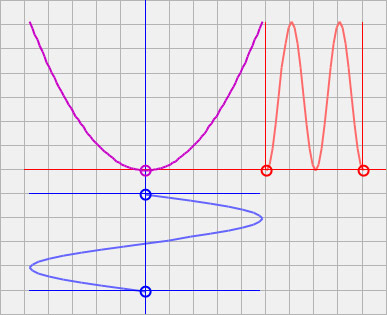
Squaring a source sub-wave's phase angle (blue), bifurcates its angular velocity (red).
The two components together form a quadratic potential well based on self-interaction,
relating the sub-waves to a particle's mass (bifurcated wave's magnitude).


If the bifurcation is synchronized (which is the case for perceptual states and for harmonic entities), the quadratic part of a potential well is formed specifically by distinct, positively bifurcated sub-wave phase pairs of the resp. constituent waves. A phase pair couples the charge with a resp. Dirac spinor.

The temporal bifurcation is effectively a gauge phenomenon, indicating that the ever present, implicit (principal or axiomatic) bifurcation of the sub-stratum (also, the "swabhava" in philosophy) is now explicitly being realized as a known resp. perceived state. This known state, in its most rudimental form, is a hydrogen atom.


3 source sub-waves
4 bifurcated sub-waves, with potential wells and Dirac spinors
sub-wave #
wave number
angular velocity
1
Phi^0 = 1
1
2
Phi^1 = Phi
1
3
Phi^2
1
sub-wave # wave number angular velocity
0 - electron Phi^2 - Phi - 1 = 0 +1 - 1 - 1 = {-1}
1 - photon (Phi^2) - Phi + (1) = 2 · 1 (+1) - 1 (+ 1) = [{2} - 1] = 1
     
2 - gluon (Phi^2 + Phi) - 1 = 2 · Phi (1 + 1) - 1 = [{2} - 1] = 1
3 - quarks Phi^2 + Phi + 1 = 2 · Phi^2 1 + 1 + 1 = {3}

Integral bifurcation table, with emphasis on temporal bifurcation and potential well. The paired sub-waves
constituting the quadratic, charged sphere are in round brackets. The factors 2 in the angular velocities show the
phase bifurcation. The potential wells are in square brackets, while {2,3} and {2,-1} are the resp. Dirac spinors.



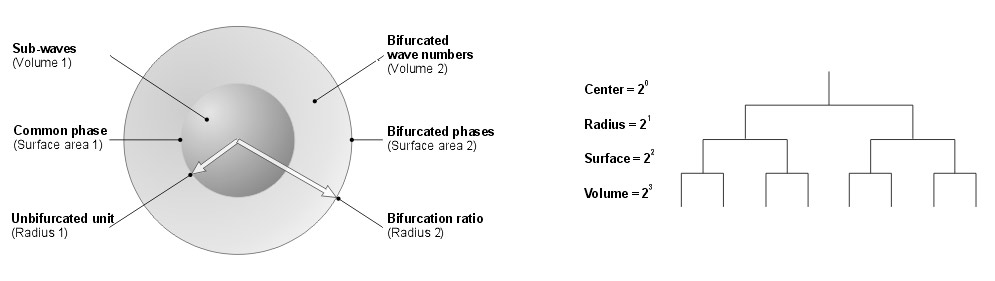
The spherical potential well and bifurcation scheme (both simplified)
Note that it should not too literally be viewed as an atom model.



MOVE OVER OR TAP IMAGE TO START
Bifurcation tree, scaling to synchronization


In summary, it was shown that the bifurcation of sub-waves consists of a spectrum analysis of the source wave numbers in space, and a topological analysis of the common phase cycle in time. The space- and time bifurcation together constitutes a dimensional analysis, in the form of a spherical potential well.

 


BACK TO MICROVITA.INFO